Table of Contents
Introducción
En este artículo, veremos el modelo de Regresión Lineal para el Machine Learning, que es uno de los modelos más básicos disponibles.
Regresión Lineal
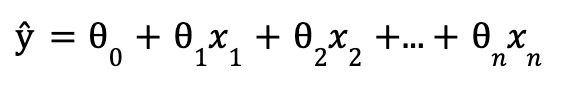
Esta ecuación muestra una fórmula multidimensional para la regresión lineal, donde ŷ es el valor multidimensional predicho, n es el número de dimensiones (o comúnmente llamadas características),xi es el ith valor de la característica, y ⍬ es el jth parámetro o peso del modelo.
Con esta definición, ahora debemos ver la forma de entrenar un modelo siguiendo esta ecuación. Entrenar un modelo significa ajustar sus parámetros para que el modelo se ajuste lo mejor posible al conjunto de entrenamiento. También debemos encontrar una medida de lo bien que el modelo se ajusta a los datos de entrenamiento, para ello podríamos utilizar el Error Cuadrático Medio (MSE).
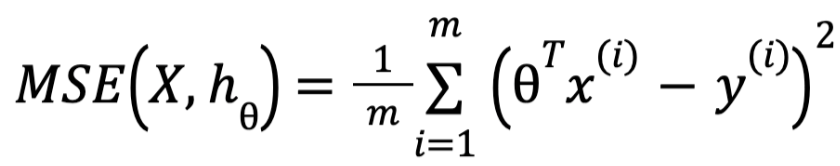
Aquí estamos usando x, y, ⍬ como vectores de tamaño m.
Teniendo esto en cuenta, para entrenar un modelo de Regresión Lineal necesitamos encontrar el valor de ⍬ que minimice el MSE.
Ecuación Normal
Existe una solución de forma cerrada llamada Ecuación Normal que da el valor de ⍬ que minimiza la función de coste.
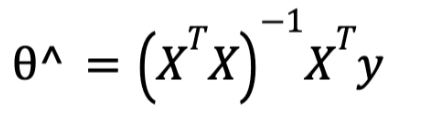
Donde ⍬^es el valor de ⍬ que minimiza la función de coste, y es el vector de valores objetivo que contiene y¹a ym
Veamos un ejemplo con datos de aspecto lineal para probar esta ecuación:
Ahora podemos calcular ⍬^utilizando la Ecuación Normal:
Como podemos ver la ecuación inicial que hemos utilizado para generar los datos es:
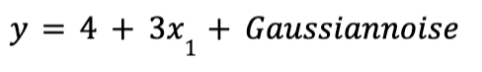
Y podíamos haberlo esperado:
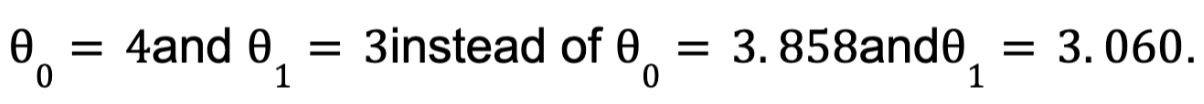
El resultado se aproximaba bastante, sin embargo, el Gaussian noise hacía imposible recuperar los parámetros exactos de la función original. Ahora podemos hacer predicciones utilizando ⍬^:
Existen varias herramientas de ML para realizar la Regresión Lineal en lugar de calcular estas ecuaciones manualmente, por ejemplo, Scikit-Learn:
Coeficiente de correlación estándar
El coeficiente de correlación estándar, también llamado de Pearson, nos da una medida de la correlación lineal entre dos conjuntos de datos. Es el cociente entre la covarianza de dos variables y el producto de sus desviaciones típicas:
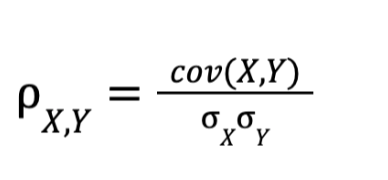
Este coeficiente varía entre -1 y 1. Cuanto más se acerque a 1 o -1, más correlacionadas estarán las dos variables (positivas o negativas).
Podemos calcular este coeficiente fácilmente con Python utilizando la librería pandas. Para nuestro ejemplo, necesitamos transformar x e y en variables de una dimensión con la función concatenate de numpy y luego usando la función corr() en el conjunto de datos creado con pandas, obtenemos la matriz de correlaciones entre estos dos parámetros:
En este caso, el coeficiente de correlación entre x e y es 0,855022. Por tanto, podemos decir que están bastante correlacionadas, como era de esperar.
Regresión lineal
En esta sección, vamos a utilizar lo que hemos aprendido anteriormente para analizar un conjunto de datos sobre los precios de la vivienda en Boston. Podemos descargar el conjunto de datos de Kaggle (nos proporciona múltiples conjuntos de datos para probar y aprender).
Información sobre atributos
Características de entrada en orden:
- CRIM: tasa de delincuencia per cápita por ciudad
- ZN: proporción de suelo residencial zonificado para lotes de más de 25.000 pies cuadrados.
- INDUS: proporción de acres comerciales no minoristas por ciudad
- CHAS: Variable ficticia Charles River (1 si el tramo linda con el río; 0 en caso contrario)
- NOX: concentración de óxidos nítricos (partes por 10 millones) [partes/10M].
- RM: número medio de habitaciones por vivienda
- AGE: proporción de unidades ocupadas por sus propietarios construidas antes de 1940
- DIS: distancias ponderadas a cinco centros de empleo de Boston
- RAD: índice de accesibilidad a las autopistas radiales
- TAX: tipo del impuesto sobre bienes inmuebles de valor íntegro por 10.000 $ [10.000 $].
- PTRATIO: ratio alumnos-profesor por ciudad
- B: El resultado de la ecuación B=1000(Bk – 0,63)^2 donde Bk es la proporción de negros por ciudad
- LSTAT: % estatus inferior de la población
- MEDV: Valor medio de las viviendas ocupadas por sus propietarios en miles de $ [k$].
Nuestro objetivo será ver la correlación entre los precios y otras variables del conjunto de datos, utilizando el coeficiente de correlación estándar. Primero cargamos el conjunto de datos utilizando pandas:
Ahora podemos ver cómo se correlaciona cada atributo con el valor medio de las viviendas ocupadas por sus propietarios:
El coeficiente de correlación varía entre 1 y -1. Cuando se aproxima a 1, significa que existe una fuerte correlación positiva. En este caso, el precio tiende a subir cuando sube el RM (número medio de habitaciones por vivienda). Podemos ver que el coeficiente de correlación es 0,695 y como observamos en el gráfico a pesar de algunos puntos existe una fuerte correlación entre estas dos características.
Conclusión
Hemos visto los fundamentos de la regresión lineal y sus aplicaciones al Machine Learning. Hemos aprendido a predecir nuevos valores con modelos de regresión lineal y también hemos visto cómo utilizar la matriz de coeficientes de correlación estándar para obtener características correlacionadas en conjuntos de datos.
Author
More to Explore












